Answer:
True
Explanation:
By changing both equations to slope-intercept, it is easier to determine whether two lines are perpendicular.
Since
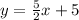 is already in slope-intercept form, we just need to change the first given equation.
is already in slope-intercept form, we just need to change the first given equation.
2x + 5y + 3 = 0
2x + 5y = -3
5y = -2x -3
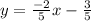
Two lines are perpendicular when the slope of the lines (coefficient of x) are negative reciprocals (opposite sign of the inverse of a number).
Comparing the two slopes
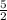 and
and
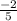 , we can see they they both fit the criteria of being opposite signs and inverses of each other.
, we can see they they both fit the criteria of being opposite signs and inverses of each other.
So 2x + 5y + 3 = 0 is perpendicular to y = (5/2)x+ 5.