Question

Meldie made a cube whose side is (3x - 2) inches. Find its volume in cubic inches.

Answer 1

x^2(3x-2) cubic inches OR in^3

OR

3x { 3 [ 3x ( x - 2 ) + 4 ] } - 8 cubic inches OR in^3

I AM UNAWARE IF YOU ASKED THAT ONE SIDE IS (3X-2) OR ALL. I WILL ANSWER BOTH PARTS

-

NOTE: '^' MEANS TO THE POWER OF..

-

Volume = v, abc = 3 sides of cube (height, width, length)

Using the formula for volume in a cube,

`v = abc`

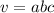
We can solve this.

If one side is (3x-2)in,

• (3x-2)(x)(x) = v.... x are the other two sides
• x^2(3x-2) = v

x^2(3x-2) cubic inches OR in^3

If all sides are (3x-2)in,

Use the formula,

`(a - b) ^(3) = {a}^(3) + 3ab(b - a) - {b}^(3)`

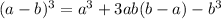
We can solve this.

• (3x-2)(3x-2)(3x-2) = v
• (3x-2)^3 = v.... 3x = a and -2 = b
• (3x)^3 + [(3)(3x)(2)][2-3x] - (2)^3 = v
• 27x^3 + 18x(2-3x) -8 = v
• (27x^3 + 36x - 54x^2) - 8 = v.. Terms inside brackets - take 3x as common and leave out 8
• 3x(9x^2 -18x +12) = v... Take 3 as common again in the brackets
• 3x [ 3 ([3x^2 -6x] + 4) -8 = v....Take 3x common in the terms in square brackets
• 3x [ 3 [ 3x (x-2) + 4 ]] - 8 = v
• 3x { 3 [ 3x ( x - 2 ) + 4 ] } - 8 = v

3x { 3 [ 3x ( x - 2 ) + 4 ] } - 8 cubic inches OR in^3

___

If you have any questions regarding formulas or anything, comment and I will get back to you asap.

___