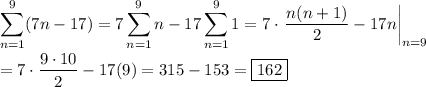Answer:
162
Explanation:
You want the sum of the first 9 terms described by ...
a[n] = 7n -17
Add the terms
There are several ways the sum can be found. Most straightforward is simply adding up the terms:
For n=1, 7n-17 = -10
For n=2, 7n -17 = -3
The remaining 7 terms are 4, 11, 18, 25, 32, 39, 46.
The sum is ...
-10 -3 +4 +11 +18 +25 +32 +39 +46 = 162
Arithmetic sequence
The terms form an arithmetic sequence with first term -10 and last term 46. The sum will be the average term multiplied by the number of terms:
((-10 +46)/2)(9) = 18(9) = 162
Sum formulas
The sum can be decomposed into the sums whose formulas we know: