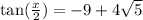Explanation:
We know rhat
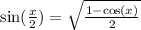
whenever x lies from 90 to 180.
If
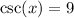
Using Reciprocal Identities
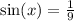
Using Pythagorean Identity,
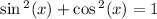
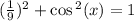
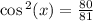
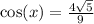
Cosine is negative in when x lies between 90 and 180 so
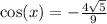
So
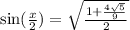
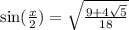
For cosine remember
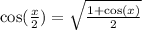
Cosine is negative in second quadrant so
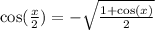
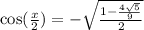
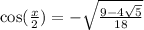
For tangent,
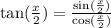
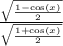
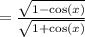
Tangent is negative over 90<x<180 so
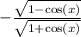
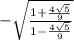

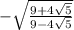
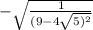
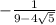
so
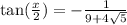
or