Answer:
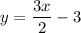
Explanation:
Before we identify the equation of the line in slope intercept form, we must identify the slope intercept form equation. The slope intercept form equation is y = (m)x + (b) ⇒ m = slope of line; b = y-intercept of line.
To identify the equation of the line shown in slope intercept form, according to the slope intercept form equation, we need to identify the slope of the line and the y-intercept of the line. The slope of a line is the rate of a line, which advances up/down/side-to-side at a constant rate. The y-intercept of a line is the intersection of the line at the y-axis.
There is a specific formula for identifying the slope:

Some facts about slope: The slope of a line will also depend on the graph. If the graph ascends upward to somewhere in Quadrant 1 or 2, the slope of the line will be positive. If the graph descends downward to somewhere in Quadrant 3 or 4, the slope will be negative. If the line horizontal and it passes perfectly through the x-axis, the slope of the line is 0. If the slope of the line is vertical, then the slope will be undefined.
Location of plotted points: First point: (0, -3); Second point: (2, 0)
Let us now identify the x and y coordinates of the plotted points:
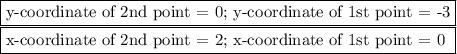
Plug the coordinates into the slope formula to determine the slope:
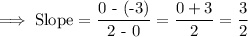
Plug the slope of the line into the slope intercept form equation:

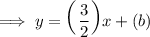
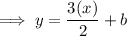
Let us plug any point (that is on the line) for x and y. This will help us find the y-intercept (b). I will plug in the first point because it is my preference.
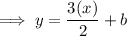
![\implies -3 = (3(0))/(2) + b \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ [\text{First point: (0, -3)} \implies x = 0; y = -3]}](https://img.qammunity.org/2023/formulas/mathematics/high-school/2ylk0gvmo1bbqb3ej90qp5s1ijrvudhf4j.png)
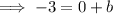
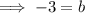
Finally, let us substitute the slope of the line and the y-intercept of the line into the slope-intercept form equation. Then, we can simplify both sides of the equation and isolate the y-variable completely on the other side.

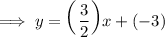
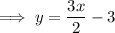
Therefore, the equation of the line in slope intercept form is y = 3x/2 - 3.