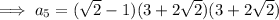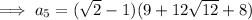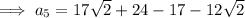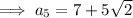Question

Answer the question in the image below.

Answer 1

(a) x = 2

(b) 7 + 5√2

Explanation:

Part (a)

Given terms of a geometric sequence:

• 
  `a_1=√(x)-1`

• 
  `a_2=1`

• 
  `a_3=√(x)+1`

The common ratio of a geometric sequence is found by dividing consecutive terms. Therefore:

`\implies (a_3)/(a_2)=(a_2)/(a_1)`

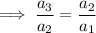
Substitute the given terms into the equation and solve for x:

`\implies (√(x)+1)/(1)=(1)/(√(x)-1)`

`\implies (√(x)-1)(√(x)+1)=1`

`\implies x+√(x)-√(x)-1=1`

`\implies x-1=1`

`\implies x=2`

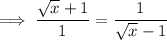
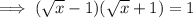
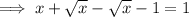
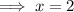
Part (b)

General form of a geometric sequence:

`\boxed{a_n=ar^(n-1)}`

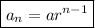
where:

• 
  `a_n` is the nth term.
• a is the first term.
• r is the common ratio.
• n is the position of the term.

Substitute the found value of x into the expressions for the given terms:

• 
  `a_1=√(2)-1`
• 
  `a_2=1`
• 
  `a_3=√(2)+1`

Find the common ratio:

`\implies r=(a_3)/(a_2)=(√(2)+1)/(1)=√(2)+1`

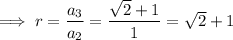
Therefore, the equation for the nth term is:

`\boxed{a_n=(√(2)-1)(√(2)+1)^(n-1)}}`

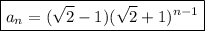
To find the 5th term, substitute n = 5 into the equation:

`\implies a_5=(√(2)-1)(√(2)+1)^(5-1)`

`\implies a_5=(√(2)-1)(√(2)+1)^(4)`

`\implies a_5=(√(2)-1)(√(2)+1)^2(√(2)+1)^2`

`\implies a_5=(√(2)-1)(3+2√(2))(3+2√(2))`

`\implies a_5=(√(2)-1)(9+12√(12)+8)`

`\implies a_5=(√(2)-1)(17+12√(2))`

`\implies a_5=17√(2)+24-17-12√(2)`

`\implies a_5=7+5√(2)`