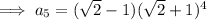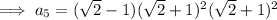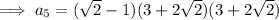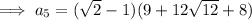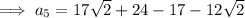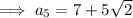Answer:
(a) x = 2
(b) 7 + 5√2
Explanation:
Part (a)
Given terms of a geometric sequence:
The common ratio of a geometric sequence is found by dividing consecutive terms. Therefore:
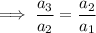
Substitute the given terms into the equation and solve for x:
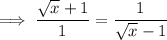
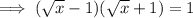
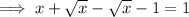

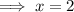
Part (b)
General form of a geometric sequence:
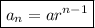
where:
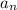 is the nth term.
is the nth term.- a is the first term.
- r is the common ratio.
- n is the position of the term.
Substitute the found value of x into the expressions for the given terms:
Find the common ratio:
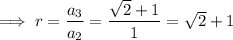
Therefore, the equation for the nth term is:
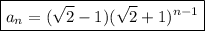
To find the 5th term, substitute n = 5 into the equation: