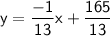Answer:
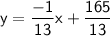
Explanation:
Equation of line in slope-intercept form: y = mx + b
Here m is the slope and b is the y-intercept.
y = 13x - 4
m₁ = 13
Product of slope of the Perpendicular line m * m₁ = -1

Equation of the line:

The point (9,12) passes through the line. Substitute the coordinates in the above equation and find the value of 'b'.
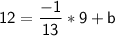

Equation of line: