Answer:
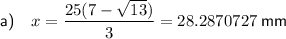
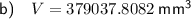
Step-by-step explanation:

Given:
The dimensions of the rectangular prism in terms of x are:
- Length = 200 - 2x
- Width = 150 - 2x
- Height = x
Substitute these values into the formula for volume to create an equation in terms of x:
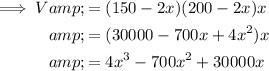
To find the value of x that will give the maximum volume, differentiate the equation for volume.
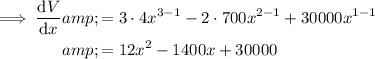
Set the derivative to zero and solve for x using the quadratic formula:
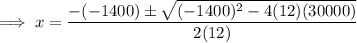
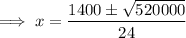
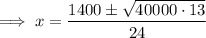
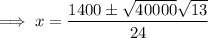

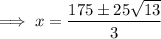
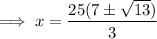
To determine which value of x will give the maximum volume, differentiate again:
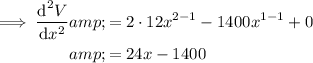
Substitute both values of x into the second derivative:
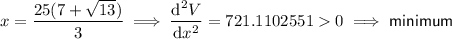
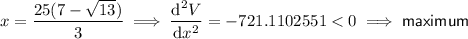
Therefore, the value of x which will give the maximum volume is:
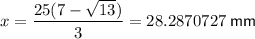
To find the maximum volume of the box, substitute the found value of x into the equation for volume:

The dimensions of the box with maximum possible volume will be:
- Length = 143.4 mm (1 d.p.)
- Width = 93.4 mm (1 d.p.)
- Height = 28.3 mm (1 d.p.)