Question

Please complete both question

this is urgent so please try and complete it as fast as possible
due today ​

Answer 1

`\textsf{a)} \quad x=(25(7-√(13)))/(3)=28.2870727\; \sf mm`

`\textsf{b)} \quad V=379037.8082\; \sf mm^3`

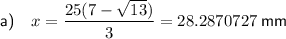
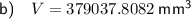
Step-by-step explanation:

`\boxed{\begin{minipage}{5 cm}\underline{Volume of a rectangular prism}\\\\$V=w\:l\:h$\\\\where:\\ \phantom{ww}$\bullet$ $w$ is the width of the base. \\ \phantom{ww}$\bullet$ $l$ is the length of the base. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

Given:

• l = 200 mm
• w = 150 mm

The dimensions of the rectangular prism in terms of x are:

• Length = 200 - 2x
• Width = 150 - 2x
• Height = x

Substitute these values into the formula for volume to create an equation in terms of x:

`\begin{aligned}\implies V&=(150-2x)(200-2x)x\\&=(30000-700x+4x^2)x\\&=4x^3-700x^2+30000x\end{aligned}`

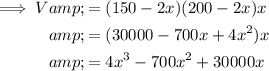
To find the value of x that will give the maximum volume, differentiate the equation for volume.

`\begin{aligned}\implies \frac{\text{d}V}{\text{d}x}&=3 \cdot 4x^(3-1)-2 \cdot 700x^(2-1)+30000x^(1-1)\\&=12x^2-1400x+30000\end{aligned}`

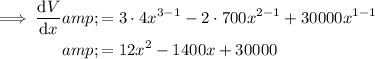
Set the derivative to zero and solve for x using the quadratic formula:

`\implies x=(-(-1400) \pm √((-1400)^2-4(12)(30000)))/(2(12))`

`\implies x=(1400 \pm √(520000))/(24)`

`\implies x=(1400 \pm √(40000 \cdot 13))/(24)`

`\implies x=(1400 \pm √(40000)√(13))/(24)`

`\implies x=(1400 \pm 200√(13))/(24)`

`\implies x=(175\pm 25√(13))/(3)`

`\implies x=(25(7\pm√(13)))/(3)`

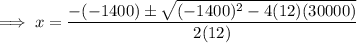
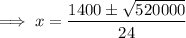
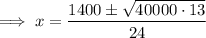
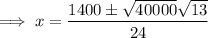
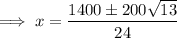
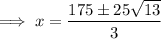
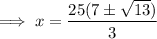
To determine which value of x will give the maximum volume, differentiate again:

`\begin{aligned}\implies \frac{\text{d}^2V}{\text{d}x^2}&=2 \cdot12x^(2-1)-1400x^(1-1)+0\\&=24x-1400\end{aligned}`

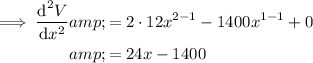
Substitute both values of x into the second derivative:

`x=(25(7+√(13)))/(3) \implies \frac{\text{d}^2V}{\text{d}x^2}=721.1102551 > 0\implies \sf minimum`

`x=(25(7-√(13)))/(3) \implies \frac{\text{d}^2V}{\text{d}x^2}=-721.1102551 < 0\implies \sf maximum`

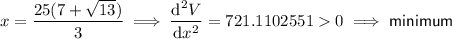
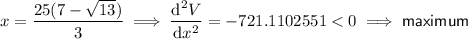
Therefore, the value of x which will give the maximum volume is:

`x=(25(7-√(13)))/(3)=28.2870727\; \sf mm`

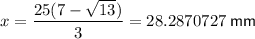
To find the maximum volume of the box, substitute the found value of x into the equation for volume:

`\begin{aligned}\implies V_(\sf max)&=4\left((25(7-√(13)))/(3)\right)^3-700 \left((25(7-√(13)))/(3)\right)^2+30000 \left ((25(7-√(13)))/(3)\right)\\\\&=379037.8082\; \sf mm^3\end{aligned}`

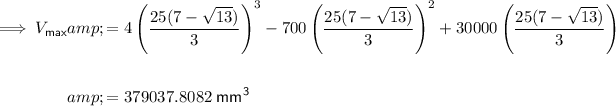
The dimensions of the box with maximum possible volume will be:

• Length = 143.4 mm (1 d.p.)
• Width = 93.4 mm (1 d.p.)
• Height = 28.3 mm (1 d.p.)