Question

Explain why square root x is not defined for all values of x .

Answer 1

⇒ Let x be treated as any real number

⇒Meaning x can be a positive number or x can be a negative number.

⇒ The square root of x can be defined ONLY if x is a non negative number, ∀ x>0 the square root is defined

For this notation
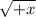`√(+x)` there exist a certain real number ..It is defined.

Let x now be a negative number.

`√(-x)`

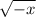
⇒For any negative number under the square root the result is an undefined number,

⇒ x and -x are all treated as VALUES (x) but NOT for all values (x) now you will find a defined number as an output.

⇒ As a conclusion for non negative x under a square root you get a defined value

⇒But for an negative number under a square root you get an undefined number as an output.

⇒Square root x may not be defined for some values x BECAUSE X CAN BE NEGATIVE..