⇒ Let x be treated as any real number
⇒Meaning x can be a positive number or x can be a negative number.
⇒ The square root of x can be defined ONLY if x is a non negative number, ∀ x>0 the square root is defined
For this notation
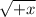 there exist a certain real number ..It is defined.
there exist a certain real number ..It is defined.
Let x now be a negative number.
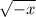
⇒For any negative number under the square root the result is an undefined number,
⇒ x and -x are all treated as VALUES (x) but NOT for all values (x) now you will find a defined number as an output.
⇒ As a conclusion for non negative x under a square root you get a defined value
⇒But for an negative number under a square root you get an undefined number as an output.
⇒Square root x may not be defined for some values x BECAUSE X CAN BE NEGATIVE..