Answer:
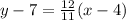
=========================================================
Step-by-step explanation:
Let's first find the slope of the line through these given points.
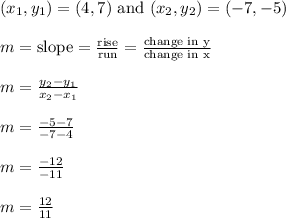
Then we'll apply point-slope to finish up the problem.

Normally we would distribute the 12/11 value through and then isolate y; however, your teacher specifically mentioned to write the answer in point-slope form.
There's nothing really special about the selection of (x1,y1) as (4,7) since we could have easily swapped the given points and used (x1,y1) = (-7,-5) instead. The order of the points does not matter.
In other words, an alternative answer would be
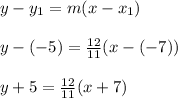
I'll stick with the first equation since (4,7) was listed first.