Answer:
(3) y-3 = -2(x + 1)
Explanation:
Lets change all equations to slope-intercept form to easily see the slope.
Slope-Intercept Form:
y = mx+b
M is slope, or the amount the y-value increases when the x-value increases by 1. B is y-intercept, or the y-value of the line when it is intersecting the y-axis (x=0).
#1: y + 5 = x - 3
Subtract 5 on both sides.
y + 5 - 5 = x - 5
Simplify.
y = x - 5
In slope intercept form. Slope of 1 and y-intercept of -5.
#2: y=2x+1
Already in slope intercept form. Slope of 2 and y-intercept of -5.
#3: y-3 = -2(x+1)
Use distributive property to simplify.
y - 3 = -2x-2
Add 3 on both sides.
y - 3 + 3 = -2x - 2 + 3
Simplify.
y = -2x+1
In slope intercept form. Slope of 2 and y-intercept of 1.
#4: y = x+2
Already in slope intercept form. Slope of 1 and y-intercept of 2.
Now using the slope formula, we can eliminate 2 possibilities.
Slope Formula:

Plug in points.

Simplify.
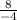
Divide.
-2
Slope is -2. Because the slopes of #1 and #4 are 1 (not -2), they cannot be the equation that passes through the line. The slope of #2 is 2, not -2. We are left with: #3.