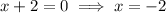Answer:
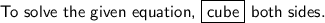
Explanation:
Given equation:
![\sqrt[3]{x^2-7} =\sqrt[3]{2x+1}](https://img.qammunity.org/2023/formulas/mathematics/high-school/m5n6qqd99v9cs64j11re4qx7984uw4folc.png)
![\textsf{Apply exponent rule} \quad \sqrt[n]{a}=a^{(1)/(n)}:](https://img.qammunity.org/2023/formulas/mathematics/high-school/zlrncj0wa7sh605f3a9919788r7yr9i2bk.png)
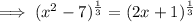
Cube both sides of the equation:
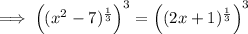

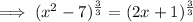
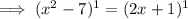
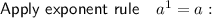
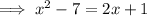
Subtract 2x from both sides:
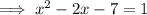
Subtract 1 from both sides:

Rewrite -2x as (-4x + 2x):

Factor the first two terms and the last two terms separately:
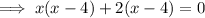
Therefore:
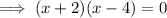
Apply the zero-product property: