Answer:
a)
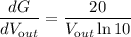
b)
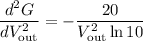
Explanation:
From the given equations to find, we are differentiating function G with respect to V out. Therefore, we will be only using the equation (6):

Here’s a fresh-up reminders for logarithmic differentiation formula:
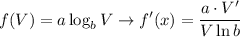
Note that V' means to derive or differentiate the V-term
Therefore, in this scenario, our values of term are:
- a = 20
- b = 10 (Since logarithm base is not shown, it’s always assumed to be common logarithm)
- V = 10V out
Therefore, we can apply differentiation formula:
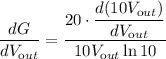
Simplify:
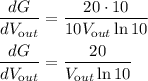
And we have finished the part a. On part b, we just differentiate the answer from part a again, the second part is to obtain the second derivative which is to derive the first derivative. Therefore:

First, separate the constant every time when you have to differentiate a function:
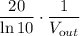
Differentiate 1/V out: recall the formula of fraction:

The formula above is derived from power rules formula where:
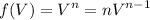
Therefore, from the function of V out:
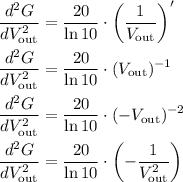
Simplify to latest as we get:
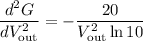
Please let me know if you have any questions!