Answer:
Line A and C
Explanation:
The perpendicular slope of another line is the negative reciprocal of the other slope.
For example, we have line
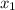 .
.
y = x
The line that is perpendicular to it is:
y=
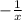
Lets tranform all of these equation to slope intercept form:
y = mx+b
M is the slope or how much the y value increases every time the x value increases by one. b is the y-intercept or when x=0.
Divide 2 on both sides to simplify line a into slope intercept form.
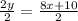
Simplify.
y = 4x + 5
Now it is in slope-intercept form. Slope of 4 and y-intercept of 5.
Line B
Isolate y on both sides by subtracting 3x on both sides.
6y + 3x - 3x = 12 - 3x
6y = 12 - 3x
Divide 6 on both sides.

Simplify.
y = -1/2x + 2
Now it is in slope-intercept form. Slope of -1/2 and y-intercept of 2.
Line C
Divide both sides by 8.
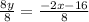
Simplify.
y = -1/4x - 2
Line A has a slope of 4. Line C has a slope of -1/4x. Line C is the negative reciprocal of Line A as multiplying Line A by -1 and flipping the fraction simple gets you Line C. (and vice versa).