Question

Anyone who understands derivatives, please help.

Answer 1

Answer to part (A) is y = 42x+9

Answer to part (B) is 98

========================================================

Step-by-step explanation:

Part (A)

Let's plug x = 0 into the 1st derivative of f(x)

`f'(\text{x}) = \cos(\pi \text{x}) + \text{x}^5 + 6\\\\f'(0) = \cos(\pi *0) + (0)^5 + 6\\\\f'(0) = 1 + 0 + 6\\\\f'(0) = 7\\\\`

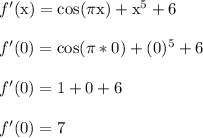
We'll use that later in the steps below, which show computing the derivative value of h(x) at x = 0.

`h(\text{x}) = ( f(\text{x}) )^2\\\\h'(\text{x}) = 2( f(\text{x}) )*f'(\text{x}) \ \ \text{ ... chain rule}\\\\h'(0) = 2( f(0) )*f'(0)\\\\h'(0) = 2( 3 )*7\\\\h'(0) = 42\\\\`

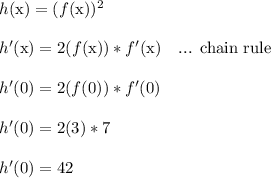
This is the slope of the tangent line to h(x) at x = 0.

Now plug x = 0 into the h(x) function itself, without any derivatives applied.

`h(\text{x}) = ( f(\text{x}) )^2\\\\h(0) = ( f(0) )^2\\\\h(0) = ( 3 )^2\\\\h(0) = 9\\\\`

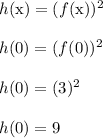
This is the y intercept of the line, i.e. the b value.

We found that

• m = 42 = slope of the tangent
• b = 9 = y intercept of the tangent line

We go from y = mx+b to y = 42x+9 as the equation of the tangent line.

===================================================

Part (B)

In the previous part, we already calculated the first derivative. Differentiate that with respect to x to get the second derivative.

`h'(\text{x}) = 2( f(\text{x}) )*f'(\text{x})\\\\h''(\text{x}) = (d)/(dx)\left[h'(x)\right]\\\\h''(\text{x}) = (d)/(dx)\left[2( f(\text{x}) )*f'(\text{x})\right]\\\\h''(\text{x}) = (d)/(dx)\left[2( f(\text{x}) )\right]*f'(\text{x})+2*f(\text{x})*(d)/(dx)\left[f'(\text{x})\right] \ \ \text{ ... product rule}\\\\h''(\text{x}) = 2f'(\text{x})*f'(\text{x})+2*f(\text{x})*f''(\text{x})\\\\h''(\text{x}) = 2\left(f'(\text{x})\right)^2+2*f(\text{x})*f''(\text{x})\\\\`

The second derivative is useful to determine where the function is concave up or concave down. And also to determine points of inflection.

The h''(x) function involves f''(x), so we'll need to find the second derivative of the f(x) function.

`f'(\text{x}) = \cos(\pi \text{x}) + \text{x}^5 + 6\\\\f''(\text{x}) = (d)/(dx)\left[\cos(\pi \text{x}) + \text{x}^5 + 6\right]\\\\f''(\text{x}) = -\pi\sin(\pi \text{x}) + 5\text{x}^4\\\\`

Then plug in x = 0

`f''(\text{x}) = -\pi\sin(\pi \text{x}) + 5\text{x}^4\\\\f''(0) = -\pi\sin(\pi *0) + 5(0)^4\\\\f''(0) = 0\\\\`

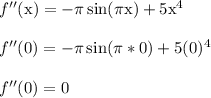
We have enough info to find h''(0) finally.

`h''(\text{x}) = 2\left(f'(\text{x})\right)^2+2*f(\text{x})*f''(\text{x})\\\\h''(0) = 2\left(f'(0)\right)^2+2*f(0)*f''(0)\\\\h''(0) = 2\left(7\right)^2+2*3*0\\\\h''(0) = 98\\\\`

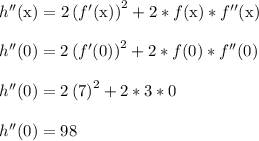
Side notes:

• Refer back to the previous section when we found f'(0) = 7.
• The h''(0) is positive. It tells us that h(x) is concave up when x = 0.