Question

`√(3^2+27)+2^3+\sqrt[3]{64}`

Answer 1

`\boldsymbol{\sf{√(3^2+27)+2^3+\sqrt[3]{64} }}`

Calculate 3 to the power of 2.

`\boldsymbol{\sf{√(9+27)+2^3+\sqrt[3]{64} }}`

Add 9 and 27.

`\boldsymbol{\sf{√(36)+2^3+\sqrt[3]{64} }}`

Find the square root of 36.

`\boldsymbol{\sf{6+2^3+\sqrt[3]{64} }}`

Calculate 2 to the power of 3.

`\boldsymbol{\sf{6+8+\sqrt[3]{64} }}`

Add 6 and 8.

`\boldsymbol{\sf{14+\sqrt[3]{64} }}`

Calculate
`\sqrt[3]{64}`

`\boldsymbol{\sf{14+4=18}}`

Answer 2

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bold{ 18}`

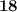
Step by step explanation:

`\: \: \: \: \: \: \: \bold{√(9 + 27) + 2 {}^(3) + \sqrt[3]{64} }`

To solve this problem, the first thing we have to do is simplify 3² to 9, since it multiplies 2 times 3 to give us 9.

`\: \: \: \: \: \: \: \: \: \: \: \: \bold{ √(36) + {2}^(3) + \sqrt[3]{64} }`

Then we must add 9 + 27 to give us a result of 36.

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bold{6 + {2}^(3) + \sqrt[3]{64} }`

Now we must multiply again but this time we are going to multiply 2 times 6 since 6 × 6 is equal to 36.

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bold{6 + 8 \: + \sqrt[3]{64} }`

Now we must again multiply 3 times 2 to give us 8.

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bold{6 + 8 + 4}`

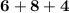
Then we must add 6 + 8 + 4.

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bold{14 + 4}`

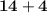
Before finishing we know that we got 14, now we must add 14 + 4 to give us a result of 18.

`\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \bold{18}`

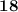
Rpt: The result is 18.