Question

Please Help!

(03.07 HC)
An architect has designed two tunnels Tunnel A is modeled by x² + y2 + 30x+ 560, and tunnel B is modeled by x2-30x+16y-95-0, where all measurements are in feet. The architect wants to verify whether a truck that is 8 feet
wide and 13.5 feet high can pass through the tunnels

Part A: Write the equation for Tunnel A in standard form and determine the conic section Show your work

Part B: Write the equation for Tunnel 8 in standard form and determine the conic section. Show your work

Part C: Determine the maximum height of each tunnel is the truck able to pass through either tunnel without damage? If so, which tunnel(s) and why? Show your work.

Answer 1

A. Circle.

`(x+15)^2+(y-0)^2=13^2`

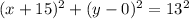
B. Parabola.

`(x-15)^2=-16(y-20)`

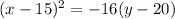
C. Maximum height of Tunnel A = 13 ft.

Maximum height of Tunnel B = 20 ft.

The truck can only pass through Tunnel B without damage.

Explanation:

`\boxed{\begin{minipage}{6.3cm}\underline{General equation for any conic section}\\\\$Ax^2+Bxy+Cy^2+Dx+Ey+F = 0$\\\\where $A, B, C, D, E, F$ are constants.\\\end{minipage}}`

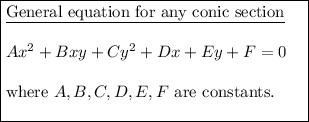
Circle: A and C are non-zero and equal, and have the same sign.

Ellipse: A and C are non-zero and unequal, and have the same sign.

Parabola: A or C is zero.

Hyperbola: A and C are non-zero and have different signs.

Part A

Tunnel A

`x^2+y^2+30x+56=0`

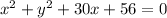
As the coefficients of x² and y² are non-zero, equal and have the same sign, the conic section is a circle.

`\boxed{\begin{minipage}{4 cm}\underline{Equation of a circle}\\\\$(x-h)^2+(y-k)^2=r^2$\\\\where:\\ \phantom{ww}$\bullet$ $(h, k)$ is the center. \\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Rewrite the given equation for Tunnel A in the standard form of the equation of a circle:

`\implies x^2+y^2+30x+56=0`

`\implies x^2+30x+y^2-56`

`\implies x^2+30x+\left((30)/(2)\right)^2+y^2=-56+\left((30)/(2)\right)^2`

`\implies x^2+30x+225+y^2=-56+225`

`\implies (x+15)^2+(y-0)^2=169`

`\implies (x+15)^2+(y-0)^2=13^2`

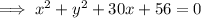
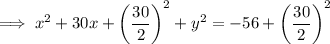
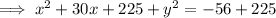
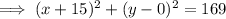
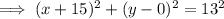
Therefore, the center of the circle is (-15, 0) and the radius is 13.

Part B

Tunnel B

`x^2-30x+16y-95=0`

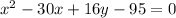
There is no term in y² so the coefficient of y² is zero. Therefore, the conic section is a parabola.

`\boxed{\begin{minipage}{5.5 cm}\underline{Standard form of a parabola}\\(with a vertical axis of symmetry)\\\\$(x-h)^2=4p(y-k)$\\\\where:\\ \phantom{ww}$\bullet$ $p\\eq 0$. \\ \phantom{ww}$\bullet$ $(h,k)$ is the vertex.\\\end{minipage}}`

Rewrite the given equation for Tunnel B in the standard form a parabola:

`\implies x^2-30x+16y-95=0`

`\implies x^2-30x=-16y+95`

`\implies x^2-30x+\left((30)/(2)\right)^2=-16y+95+\left((30)/(2)\right)^2`

`\implies x^2-30x+225=-16y+95+225`

`\implies (x-15)^2=-16(y-20)`

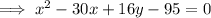
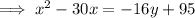
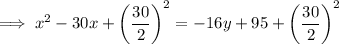
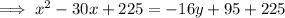
Therefore, the vertex is (15, 20).

Part C

Maximum height of Tunnel A

The maximum point of a circle is the sum of the y-value of its center and its radius:

• 
  `\textsf{Maximum height of Tunnel A}=0+13=13\; \sf feet`

Maximum height of Tunnel B

The maximum point of a downwards opening parabola is the y-value of its vertex:

• 
  `\textsf{Maximum height of Tunnel B}=20\; \sf feet`

As the truck is 13.5 feet high, it cannot pass through Tunnel A since the maximum height of Tunnel A is 13 feet.

The maximum height of Tunnel B is certainly adequate for the truck to pass through. However, to determine if the truck can pass through Tunnel B safely, we also need to find the width of the tunnel when its height is 13.5 feet. To do this, find the x-values of the parabola when y = 13.5. If the difference in x-values is 8 or more, then the truck can pass through safely.

Substitute y = 13.5 into the equation for Tunnel B and solve for x:

`\implies (x-15)^2=-16(13.5-20)`

`\implies (x-15)^2=-16(-6.5)`

`\implies (x-15)^2=104`

`\implies √((x-15)^2)=√(104)`

`\implies x-15=\pm√(104)`

`\implies x=15\pm√(104)`

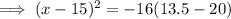
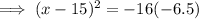
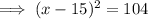
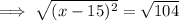
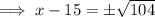
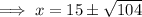
Now find the difference between the two found values of x:

`\implies (15+√(104))-(15-√(104))`

`\implies 15+√(104)-15+√(104)`

`\implies 2√(104)`

`\implies 20.39607...`

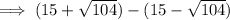
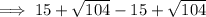
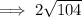
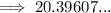
Therefore, as the width of Tunnel B is 20.4 ft when its height is 13.5 ft, the 8 ft wide truck can easily pass through without damage since 20.4 ft is greater than the width of the truck.