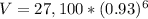Question

A new car is purchased for 27,100 dollars. The value of the car depreciates at a rate of 7% per year. Which equation represents the value of the car after 6 years?

Answer 1

Exponential Equations

In exponential relations, we can represents given values like this:

`f(x)=a*c^x`

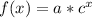
• c = growth/decay factor
• a = starting point/y-intercept

Solving the Question

We're given:

• 27,100 dollars = starting point
• Decay factor = 7% per year

⇒ Plug this information into
`f(x)=a*c^x`:

`f(x)=27,100*(0.93)^x`

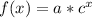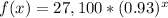
Why input 0.93 and not 0.07? Let's think of it this way: To calculate the new price of the car after one year, we find 93% of 27,100.

The dependent variable is the price (y) and the independent variable is the time in years (x).

• f(x) = price
• x = time

Therefore, to find the value of the car after 6 years, we plug in 6 as x:

`f(x)=27,100*(0.93)^6`

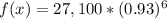
Answer

`V=27,100*(0.93)^6`