Question

NO LINKS! Please help me with this vertex problem

Show work please: step by step ​

Answer 1

`f(x)=6(x-2)^2+18`

Explanation:

Given quadratic function:

`f(x)=6x^2-24x+42`

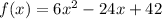
To complete the square, begin by grouping the x terms within parentheses:

`\implies f(x)=(6x^2-24x)+42`

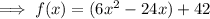
Factor out the coefficient of x²:

`f(x)=6\left(x^2-4x\right)+42`

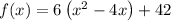
Add the square of half the coefficient of the term in x inside the parentheses, and subtract the distributed value outside the parentheses:

`\implies f(x)=6\left(x^2-4x+\left((-4)/(2)\right)^2\right)+42-6\left((-4)/(2)\right)^2`

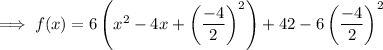
Simplify:

`\implies f(x)=6\left(x^2-4x+\left(-2\right)^2\right)+42-6\left(-2\right)^2`

`\implies f(x)=6\left(x^2-4x+4\right)+42-6\left(4)`

`\implies f(x)=6\left(x^2-4x+4\right)+42-24`

`\implies f(x)=6\left(x^2-4x+4\right)+18`

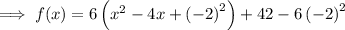
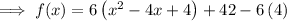
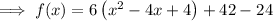
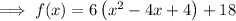
Factor the perfect square trinomial inside the parentheses:

`\implies f(x)=6(x-2)^2+18`

`\boxed{\begin{minipage}{5.6 cm}\underline{Vertex form of a quadratic equation}\\\\$y=a(x-h)^2+k$\\\\where:\\ \phantom{ww}$\bullet$ $(h,k)$ is the vertex. \\ \phantom{ww}$\bullet$ $a$ is some constant.\\\end{minipage}}`

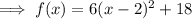
Comparing the derived equation with the vertex formula, the vertex of the derived equation is (2, 18). Hence the completion of the square is correct.