Answer:
Explanation:
This seems complicated, huh.
So think about the question. They want to know the distance from a line, to a point. first decide if the point could possibly be on the line and there is zero distance. The given point is at (-1, 7) our coordinates of the point are at -1 in the X direction and at 7 in the Y direction. If we were to plug in those two number into the given line equation, y = 3x would it be a true statement? no. 7 = 3(-1) is not true. so our given point is not on the line. Next, find the right angle to the line and point. make your own line equation that does have our given point in it. and is at a right angle to the given line. recall that using a reciprocal can give you a right angle to your line. y = (- 1/3)X . Now we just need the given point to plug into our made up line equation and be true. 7 = (-1/3)(-1) + b . we need to make this equation true by moving a number into "b" that makes it true.
b = 6
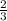 or
or
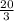
7 = (-1/3)(-1) +
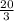
now, when does our made up line, y =(-1/3)x +
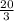 , intersect with the given line, y=3x, that is, set the two equal
, intersect with the given line, y=3x, that is, set the two equal
3x = (-1/3)x +
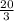
3
 X =
X =
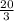
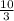 X =
X =
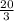
X=
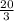 *
*
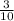
X =

X=2
our two equations intersect at 2, how handy :)
now we have our two points that are at a right angle from each other and we just need the distance from them
(given) A(-1,7) and (found) B(2,6)
Distance =
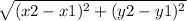
then our given points are A(x1,y1) and B(x2,y2)
Distance =
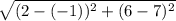
Distance =
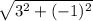
Distance =

Distance =
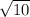
Distance = 3.1622
Distance =3.2 (rounded to nearest 10th)
Yes, that was kinda a lot :/