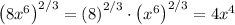(8x^(6) )^{(2)/(3) } someone explain?

Question

`(8x^(6) )^{(2)/(3) }` someone explain?

Answer 1

The first step in simplifying is to apply that outer exponent of
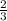`(2)/(3)` to each factor inside the parentheses.

`\left(8\cdot x^6\right)^(2/3) = \left(8\right)^(2/3) \cdot \left(x^6\right)^(2/3)`

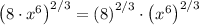
Now using the concept that
`(a)^(m/n) = \sqrt[m]{a^n}` for positive real numbers a and integers m and n, we can evaluate the first part:

`(8)^(2/3) = \sqrt[3]{8^2} = \sqrt[3]{64} =4`

For the second part, we use the power-to-a-power rule, that says
`(a^m)^n = a^(m\cdot n)`:

`\left(x^6\right)^(2/3) = x^{6\cdot (2)/(3)} = x^4`

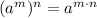Putting that all together, we have

`\left(8 x^6\right)^(2/3) = \left(8\right)^(2/3) \cdot \left(x^6\right)^(2/3) = 4x^4`

Answer 2

Explanation:

so use the properties of powers, recall that powers like
`x^{2^(2) }` is the same as
`x^(2) *x^(2)` which can also be written as
`x^(2*2)` =
`x^(4)`.

I want to make this clearer.

`x^{3^(3) }` =
`x^(3)` *
`x^(3)` *
`x^(3)` =
`x^(3*3*3)` =
`x^(27)`

I'm not sure if that's making it clearer or not.

so for your question of
`(8x^(6)) ^(2/3)` we can rewrite it to look like the above multiplication of powers

`8x^(6*(2/3))`

`(6)/(1)` *
`(2)/(3)` =
`(12)/(3)` = 4

`8x^(4)`