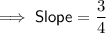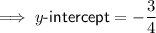Answer:
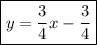
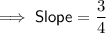
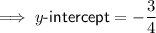
Explanation:

Given equation:
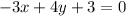
To write the given equation in slope-intercept form, rearrange the equation to isolate y.
Add 3x to both sides of the equation:
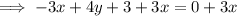
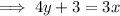
Subtract 3 from both sides of the equation:
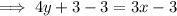
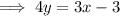
Divide both sides of the equation by 4:
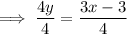
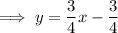
Compare the rearranged equation with the slope-intercept formula: