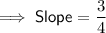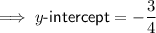Question

Anyone good there at math? Explain briefly​ and give examples

Answer 1

`\boxed{y=(3)/(4)x-(3)/(4)}`

`\implies \textsf{Slope}=(3)/(4)`

`\implies \textsf{$y$-intercept}=-(3)/(4)`

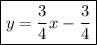
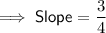
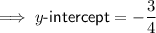
Explanation:

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

Given equation:

`-3x+4y+3=0`

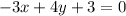
To write the given equation in slope-intercept form, rearrange the equation to isolate y.

Add 3x to both sides of the equation:

`\implies -3x+4y+3+3x=0+3x`

`\implies 4y+3=3x`

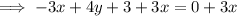
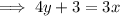
Subtract 3 from both sides of the equation:

`\implies 4y+3-3=3x-3`

`\implies 4y=3x-3`

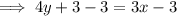
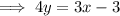
Divide both sides of the equation by 4:

`\implies (4y)/(4)=(3x-3)/(4)`

`\implies y=(3)/(4)x-(3)/(4)`

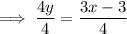
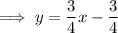
Compare the rearranged equation with the slope-intercept formula:

`\implies \textsf{Slope}=(3)/(4)`

`\implies \textsf{$y$-intercept}=-(3)/(4)`

Answer 2

• y = (3/4)x - 3/4

=====================

Slope-intercept form is:

• y = mx + b, where m- the slope, b- the y-intercept

Given line in standard form:

• - 3x + 4y + 3 = 0

Convert this to slope-intercept form:

• - 3x + 4y + 3 = 0
• 4y = 3x - 3
• y = (3/4)x - 3/4