Step-by-step explanation:

Moving all the expression to the Left side of the equation,

To find the discriminant of the above equation we can simply use the Quadratic formula.
The discriminant formula of a quadratic equation
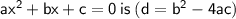
Where d represents the discriminant
a, b and c are the coefficient of the above equation,
p^2, here coefficient of p² is a = 1
-18p, here coefficient of p is b = -18
81, here the number is constant so coefficient is c = 81.
So simply by substituting the value of a, b and c in the above discriminant formula we get,
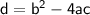
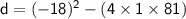
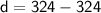
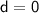
Therefore, The discriminant of 18p = p² + 81 is 0.