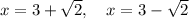Answer:
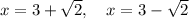
Explanation:
Given quadratic equation:
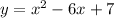
To complete the square, begin by adding and subtracting the square of half the coefficient of the term in x:
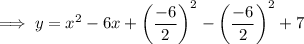
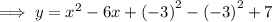
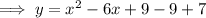
Factor the perfect square trinomial:
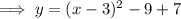
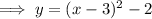
To solve the quadratic, set it to zero and solve for x:
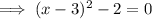
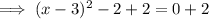

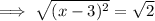
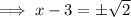
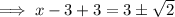
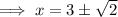
Therefore, the solution to the given quadratic equation is: