Question

State the value of the y- intercept and hence find the equation of the straight line passing through the points A and B in each of the following cases.

Answer 1

I'll do the first two parts, (a) and (b), to get you started.

===========================================================

Part (a)

First we need the slope.

`A = (x_1,y_1) = (-2,-4) \text{ and } B = (x_2,y_2) = (1,2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (2 - (-4))/(1 - (-2))\\\\m = (2 + 4)/(1 + 2)\\\\m = (6)/(3)\\\\m = 2\\\\`

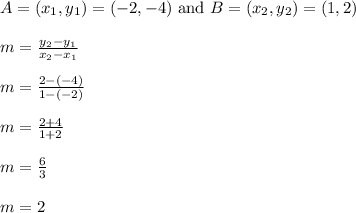
The slope is 2.

Then apply point-slope form to get the following

`y - y_1 = m(x - x_1)\\\\y - (-4) = 2(x - (-2))\\\\y + 4 = 2(x + 2)\\\\y + 4 = 2x + 2*(2)\\\\y + 4 = 2x + 4\\\\y = 2x + 4 - 4\\\\y = 2x\\\\`

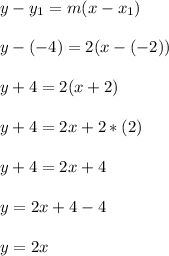
Answer: y = 2x

slope = 2

y intercept = 0

===========================================================

Part (b)

We follow the same idea as part (a).

Find the slope first.

`A = (x_1,y_1) = (-6,-2) \text{ and } B = (x_2,y_2) = (0,2)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (2 - (-2))/(0 - (-6))\\\\m = (2 + 2)/(0 + 6)\\\\m = (4)/(6)\\\\m = (2)/(3)\\\\`

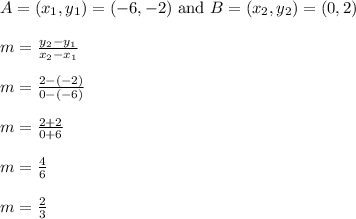
Then apply point-slope form, and solve for y.

y - y1 = m(x - x1)

y - (-2) = (2/3)(x - (-6))

y + 2 = (2/3)(x + 6)

y + 2 = (2/3)x + (2/3)(6)

y + 2 = (2/3)x + 4

y = (2/3)x + 4 - 2

y = (2/3)x + 2 is the answer

slope = 2/3

y intercept = 2