Answer:
a) R = 47.28 R = 312.73 b) 6.67
Explanation:
a)
Use the sine rule to calculate angle PRQ
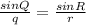
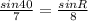
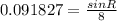
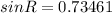
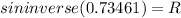
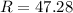
2nd angle for PRQ is 360 - 47.28 = 312.73
b) Use the cosine rule to find side p
p² = r² + q² - 2rqcosP
To find the angle of p we will simply subtract angle R and angle Q from 180.
180 - 47.28 - 40 = 92.72
p² = 8² + 7² + 2(8)(7)cos(92.72)
p² = 107.685
p = √107.685
p = 10.38
Let's suppose that the shortest distance of R from PQ is
 .
.
look at the diagram I gave
since the line I made makes a right angled triangle, we can use SOH CAH TOA
for the angle 40,
 is opposite and 10.38 is hypotenuse
is opposite and 10.38 is hypotenuse
which means we will have to use SOH
sin40 = O/H
sin40 =
 /10.38
/10.38
0.6428 =
 /10.38
/10.38
0.6428 × 10.38 =

 = 6.67
= 6.67