Question

What is the simplified form of (2/3)^3


PLEASE HURRY

Answer 1

`= > ( (2)/(3) {)}^(3)`

`= > ( (2)/(3) * (2)/(3 ) * (2)/(3) )`

`= > ( (2 * 2 * 2)/(3 * 3 * 3) )`

`= > (2 * 2 * 2)/(3 * 3 * 3)`

`= > (8)/(27)`

Answer 2

`\boxed{\tt \cfrac{8}{27} }`

OR,

`\boxed{\tt ≈\: 0.296}`

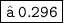
Explanation:

Given arithmetic expression:-

`\bigg({ \cfrac{2}{3} } \bigg)^(3)`

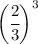
We need to find the simplified form of the given arithmetic expression.

Solution:-

In words, the question may be represented as 2/3 raised to the power of 3.

`\sf \implies\bigg({ \cfrac{2}{3} } \bigg)^(3)`

`\sf \implies \: \bigg( {\cfrac{2}{3} \bigg) }^{} * \bigg( {\cfrac{2}{3} \bigg) }^{} * \bigg( {\cfrac{2}{3} \bigg) }^{}`

It Can be rewritten as,

`\sf \implies \cfrac{2 * 2 * 2}{3 * 3 * 3}`

Multiply it :-

`\sf \implies \cfrac{4* 2}{9* 3}`

`\sf \implies \: \cfrac{8}{27}`

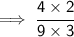
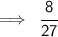
In Decimal:-

`\sf\implies\: 0.296`

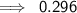
Hence, the simplest form of the arithmetic expression [exponent] is 8/27.

________________________________

I hope this helps!

Let me know if you have any questions.