let's say "x" is the original price, now let's reduce it by 25%
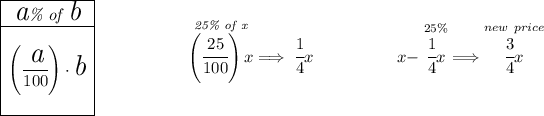
so the new price after applying a 25% or namely 1/4 of "x" is just 3/4 of "x".
if we apply the same reduction again, we'll be left with only 3/4 of ( (3/4)x ) and so on, check the picture below which shows the value once we apply the 1/4 four times, we end up with the new price being to 3/4 of whatever it was before, so

now, since we know the 100% or original price was 37, what's the new reduced price of 2997/256 off of it in percentage?
![\begin{array}{ccll} amount\%\\ \cline{1-2} 37&100\\[1em] (2997)/(256)&p \end{array}\implies \cfrac{37}{~~ (2997 )/(256 ) ~~}=\cfrac{100}{p}\implies \cfrac{(37)(256)}{2997}=\cfrac{100}{p} \\\\\\ (37)(256)p=299700\implies p=\cfrac{299700}{(37)(256)}\implies p\approx \stackrel{\%}{31.64}~\hfill \underset{savings}{\stackrel{100\%~~ - ~~31.64\%}{\approx\text{\LARGE 68.36\%}}}](https://img.qammunity.org/2023/formulas/mathematics/college/tvif3e4ky9sieyro5o9znl9feazgmiqokh.png)