Answer:
y = -0.5x + 7
Explanation:
Equation of a Line is y = mx + c
where m is the slope and c is the y-intercept
Given two lines are Perpendicular
Then
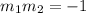
So we given Line whose Equation is y = 2x +8
Then
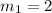 (Coefficient of x)
(Coefficient of x)
Since the Line we want is Perpendicular to that line
Then
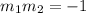 ,
,
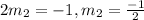
So the Equation of the required Line is y = -0.5x +c
Since the Line passes through (2 , 6) , Then y = 6 when x = 2
By substitution , 6 = -0.5*2 + c , 6 = -1 + c
Then c = 6+1 =7
Then the Equation will be y = -0.5x + 7