Answer:
a. x = 1.75, x = 4.25
b. y = -7
c. Maximum point at (3, 5).
d. Domain: (-∞, ∞)
e. Range: (-∞, 5]
f. See attachment.
Explanation:
Given function:
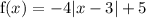
As per the question, use a graphing calculator to graph the given function.
Part a
The x-intercept(s) are the points at which the curve crosses the x-axis.
- x-intercepts: x = 1.75, x = 4.25
Part b
The y-intercept is the point at which the curve crosses the y-axis.
Part c
From inspection of the graph:
Part d
The domain of a function is the set of all possible input values (x-values).
The domain of the given function is unrestricted.
Part e
The range of a function is the set of all possible output values (y-values).
As the function has a maximum point at y = 5, the range is restricted.
Part f
Graph label the axes using a scale of 1 (see attachment).
- Plot the maximum point (3, 5).
- Plot the y-intercept: (0, -7).
- Draw a straight line from the maximum point through the y-intercept.
Substitute x = 5 into the function to find the value of y at that point:
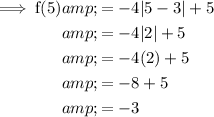
- Plot found point (5, -3).
- Draw a straight line from the maximum point through point (5, -3).