Answer:
![\huge{ \boxed{r =100( \sqrt[n]{ (A)/(P) } - 1)}}](https://img.qammunity.org/2023/formulas/mathematics/college/u0pvb8e37j4hx76lhxq1o4zsyadmami7kx.png)
Explanation:
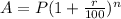
First of all in order to make r the subject we have to first divide both sides of the equation by P
That's
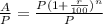
We'll finally get
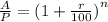
Next we have to remove the power n and to do that we find the square root of 'n' of both sides as
We have
![\sqrt[n]{ (A)/(P) } = \sqrt[n]{( {1 + (r)/(100) })^(n) } \\ \\ \\ \sqrt[n]{ (A)/(P) } = 1 + (r)/(100)](https://img.qammunity.org/2023/formulas/mathematics/college/85paetmawa8l3dk6wi30iodxktlaa20wba.png)
Next we subtract 1 from both sides to isolate r/100
We have
![\sqrt[n]{ (A)/(P) } - 1 = 1 - 1 + (r)/(100) \\ \sqrt[n]{ (A)/(P) } - 1 = (r)/(100)](https://img.qammunity.org/2023/formulas/mathematics/college/ycb0wwca5enu48sudtlk9anedqkh2azp3r.png)
Finally to isolate r , we multiply both sides by 100
![(r)/(100) * 100 =100 * (\sqrt[n]{ (A)/(P) } - 1)](https://img.qammunity.org/2023/formulas/mathematics/college/nv9gzfqxa1c2dixzzpklhfn2askgs0lhh8.png)
We have the final answer as
![r =100( \sqrt[n]{ (A)/(P) } - 1) \\](https://img.qammunity.org/2023/formulas/mathematics/college/kj7ga0tzckojic57agnnloagk3ppwa5fcd.png)
Hope this helps you