Question

A=P(1+r/100)^n express r in terms of A,P, and n​

Answer 1

`\huge{ \boxed{r =100( \sqrt[n]{ (A)/(P) } - 1)}}`

Explanation:

`A = P(1 + (r)/(100) )^(n) \\`

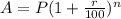
First of all in order to make r the subject we have to first divide both sides of the equation by P

That's

`(A)/(P) = \frac{P( {1 + (r)/(100) })^(n) }{P} \\`

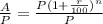
We'll finally get

`(A)/(P) = ( {1 + (r)/(100)) }^(n) \\`

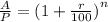
Next we have to remove the power n and to do that we find the square root of 'n' of both sides as

We have

`\sqrt[n]{ (A)/(P) } = \sqrt[n]{( {1 + (r)/(100) })^(n) } \\ \\ \\ \sqrt[n]{ (A)/(P) } = 1 + (r)/(100)`

Next we subtract 1 from both sides to isolate r/100

We have

`\sqrt[n]{ (A)/(P) } - 1 = 1 - 1 + (r)/(100) \\ \sqrt[n]{ (A)/(P) } - 1 = (r)/(100)`

Finally to isolate r , we multiply both sides by 100

`(r)/(100) * 100 =100 * (\sqrt[n]{ (A)/(P) } - 1)`

We have the final answer as

`r =100( \sqrt[n]{ (A)/(P) } - 1) \\`

Hope this helps you