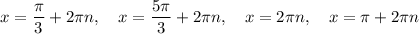Answer:
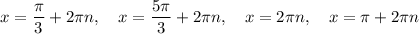
Explanation:

Given equation:
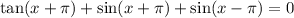
Simplify using the double angle identities:
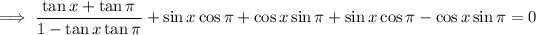
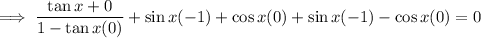
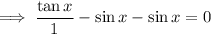

Use the tan identity to rewrite tan(x) in terms of sin(x) and cos(x):
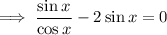
Multiply both sides by cos(x):
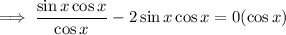
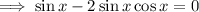
Factor out sin(x) from the left side of the equation:

Apply the zero-product property.
Case 1
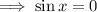
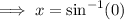
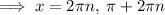
Case 2
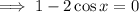
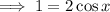
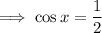
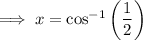
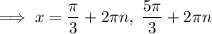
Solution