Answer: Center: (-3, 2). Radius: 4.
Explanation:
The x-coordinate of the center of the circle is given by the constant within the parenthesis with variable x. Whatever number makes the equation x + 3 = 0 is the x-coordinate of the center of the circle, which in this case is -3.
The y-coordinate of the center of the circle is given by the constant within the parenthesis with variable y. Whatever number makes the equation y - 2 = 0 is the y-coordinate of the center of the circle, which in this case is -2.
The radius of the circle is the square root of the constant on the other side of the equation. So, r =
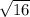 = 4.
= 4.
The explanation is from the equation of a circle in a graph:
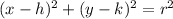
h and k in this equation stand for the coordinates of the center of the circle, with h being the x-coordinate and k being the y-coordinate. IN your equation, we have:
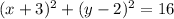
Which can also be written as
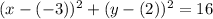
See the correlation of numbers -3 and 2 with h and k?
Notice also how the equation contains
 , so to find the radius you do
, so to find the radius you do
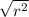 .
.