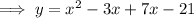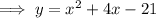Question

Write a quadratic equation in standard form given zeros {-7,3}

Answer 1

`y=x^2+4x-21`

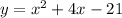
Explanation:

`\boxed{\begin{minipage}{6 cm}\underline{Factored form of a quadratic equation}\\\\$y=a(x-p)(x-q)$\\\\where:\\ \phantom{ww}$\bullet$ $p$ and $q$ are the zeros. \\ \phantom{ww}$\bullet$ $a$ is the leading coefficient.\\\end{minipage}}`

Given zeros:

• -7 and 3

Substitute the given zeros into the formula:

`\implies y=a(x-(-7))(x-3)`

`\implies y=a(x+7)(x-3)`

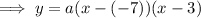
The value of "a" will not change the zeros, therefore let "a" equal any value:

`\implies y=1(x+7)(x-3)`

`\implies y=(x+7)(x-3)`

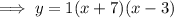
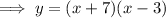
Standard form of a quadratic equation:

`\boxed{y=ax^2+bx+c}`

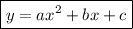
Therefore, to write the equation in standard form, expand the brackets and simplify:

`\implies y=x(x-3)+7(x-3)`

`\implies y=x^2-3x+7x-21`

`\implies y=x^2+4x-21`

Answer 2

• y = x² + 4x - 21

=============================

Quadratic equation with zeros x₁ and x₂ is:

• y = (x - x₁)(x - x₂)

And the standard form is:

• y = ax² + bx + c

Substitute zeros and convert the equation to standard form:

• y = (x - (-7))(x - 3)
• y = (x + 7)(x - 3)
• y = x² - 3x + 7x - 21
• y = x² + 4x - 21