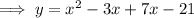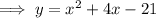Answer:
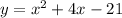
Explanation:

Given zeros:
Substitute the given zeros into the formula:
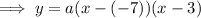
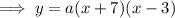
The value of "a" will not change the zeros, therefore let "a" equal any value:
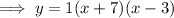
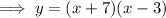
Standard form of a quadratic equation:
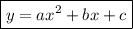
Therefore, to write the equation in standard form, expand the brackets and simplify: