Given,
The length of the whole shape is 13 inches.
The length of the cuboidal part is 8 inches.
The length of the pyramid part is 13- 8= 5 inches.
The side of the base of the both part is 6 inches.
The expression for the volume of the cuboidal part is,
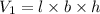
The expression for the volume of the pyramid part is,
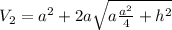
The volume of the whole shape is,
![\begin{gathered} \text{Volume =V}_1+V_2 \\ \text{ =l}* b* h+a^2+2a\sqrt{(a^2)/(4)+h^2} \\ \text{ =8}*6*6+(6)^2+2*6\sqrt[]{(6^2)/(4)+5^2} \\ \text{ =288}+36^{}+12\sqrt[]{\frac{36^{}}{4}+25} \\ \text{ =288}+36^{}+12\sqrt[]{9+25} \\ \text{ = 288}+36^{}+12*5.83 \\ \text{ =393.971 inches}^3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/x8wv4j8gv6lomz4s02vm0rk3jaqh4rpchy.png)
Hence, the volume of the shape is 393.971 inches cube.