Two numbers differ by 7.If their product is 120, find the number
Let
x and y the numbers
we have
x-y=7 ------> x=7+y -----> equation A
x*y=120 ----> equation B
solve the system
substitute equation A in equation B
(7+y)*y=120
solve for y
y^2+7y-120=0
solve the quadratic equation by graphing
the solutions are
y=8 and y=-15
Find out the value of x
For y=8
x=7+8=15
For y=-15
x=7+(-15)
x=-8
therefore
the numbers are
8 and 15 or -8 and -15
Problem N 2
we have that
EF=9 cm ----> given
EF=EH+HF ----> by addition segment postulate
substitute given values
9=x+HF
HF=(9-x) cm
step 1
In the right triangle EDH
Applying the Pythagorean Theorem
ED^2=EH^2+DH^2-----> DH^2=ED^2-EH^2
DH^2=(x+3)^2-x^2 ------> equation A
step 2
In the right triangle DHF
Applying the Pythagorean Theorem
DF^2=HF^2+DH^2 -----> DH^2=DF^2-HF^2
DH^2=(2x)^2-(9-x)^2 ------> equation B
step 3
equate equation A and equation B
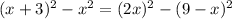
Simplify
x^2+6x+9-x^2=4x^2-(81-18x+x^2)
6x+9=4x^2-81+18x-x^2
6x+9=3x^2+18x-81
3x^2+18x-81-6x-9=0
3x^2+12x-90=0 -------> quadratic equation
step 4
Solve for x
Complete the square
3x^2+12x=90
Factor 3
3(x^2+4x)=90
simplify
(x^2+4x)=30
x^2+4x+4=30+4
rewrite as perfect squares
(x+2)^2=34
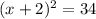
take the square root both sides
![\begin{gathered} x+2=\pm\sqrt[]{34} \\ x=-2\pm\sqrt[]{34} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/eynutnahynwh6bxl04defe77tqt30jcv09.png)
The value of x must be a positive value
therefore
![\begin{gathered} x=-2+\sqrt[]{34} \\ x=3.83\text{ cm} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/qc7kxtcrpdax7drxmooy4mpwo9rdgzitaq.png)