Before we start let's remember two important properties of integrals
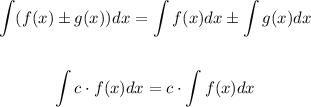
Using that, we can rewrite
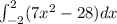
as
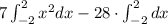
The integral of a monomial is
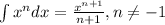
Using it let's integrate the two monomials
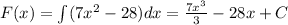
Using that and the Fundamental Theorem of Calculus:
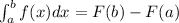
We just gotta evaluate F(x) at 2 and -2.
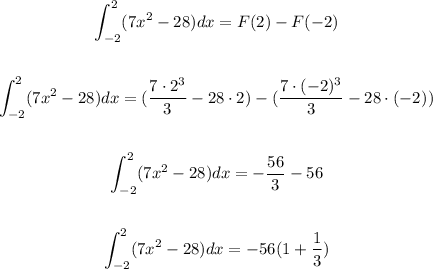
Therefore, the final result is
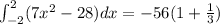
That's the signed area.