Write out the general formula for finding the volume of a cone and a cylinder
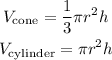
Write out the given parameter in the question

Substitute the given into the formula
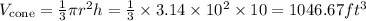
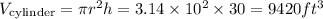
The volume of the silo is the addition of the volume of the cone and the volume of the cylinder
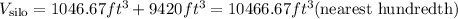
Hence, the volume of the silo is 10466.67ft³