Question

I only need the answer to question 1. Attached as a screenshot.

Answer 1

3Part 1.

The critical values occur when

`g^(\prime)(x)=0`

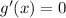
In our case, we have

`(x^2-16)/(x-2)=0`

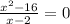
Then, for x different from 2, this last equation yields

`\begin{gathered} x^2-16=0 \\ or\text{ equivalently} \\ (x+4)(x-4)=0 \end{gathered}`

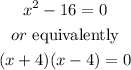
Therefore, the answer for part 1 is: x= 4 and x=-4

Part 2.

In order to see if the last points correspond to a minimum or maximim, we need to compute the seconde derivative of g. It is given by

`\begin{gathered} g^(\doubleprime)(x)=((x-2)(2x)-(x^2-16))/((x-2)^2) \\ or \\ g^(\doubleprime)(x)=((x-2)(2x)-(x+4)(x-4))/((x-2)^2) \end{gathered}`

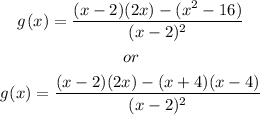
Now, lets substitute the value x=4. It yields

`\begin{gathered} g^(\doubleprime)(4)=((4-2)(2\cdot4)-(4+4)(4-4))/((4-2)^2) \\ g^(\doubleprime)(4)=((2)(8)-0)/(4) \\ g^(\doubleprime)(4)=4 \end{gathered}`

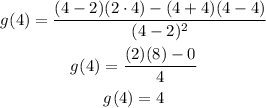
and by substituting x= -4, we have

`\begin{gathered} g^(\doubleprime)(-4)=((-4-2)(2\cdot(-4))-(-4+4)(-4-4))/((-4-2)^2) \\ g^(\doubleprime)(-4)=((-6)(-8)-0)/((-6)^2) \\ g^(\doubleprime)(-4)=(48)/(36)=(24)/(18)=(12)/(9)=(4)/(3) \end{gathered}`

Since both solutions are greater than zero, they both correspond to a local minimum points.

Part 3.

From the last result, we can see that, on the interval

S