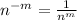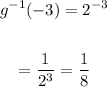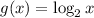
You evaluate the equation in the given values of x:
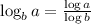
1. g(5)
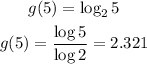
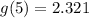
2. g(-3)
![\begin{gathered} g(-3)=\log _2(-3) \\ g(-3)=(\log (-3))/(\log 2)=\text{undefined} \end{gathered}]()
The logarithm of a negative number is undefined
3. g^-1(x)
To find the inverse function you:
-write the function with x and y:
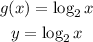
-Solve variable x:
knowing that:
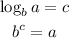
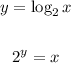
- Change the x for (g^-1(x)) and the y for x:
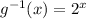
4.g^-1(-3)
As: