Question

In this diagram, lines AC and DE are parallel, and line DC is AC || DE, DC I DE, DC 1 AC,perpendicular to each of them. What is a reasonable estimate segment DE has length 1for the length of side DE?

Answer 1

Using pythagorean theorem to find AC,

`\begin{gathered} (AB)^2=(AC)^2+(BC)^2 \\ \text{Where AB=5 and BC=4} \end{gathered}`
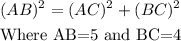
`\begin{gathered} 5^2=(AC)^2+4^2 \\ 25=(AC)^2+16 \\ (AC)^2=25-16 \\ (AC)^2=9 \\ (AC)=\sqrt[]{9} \\ (AC)=3\text{ units} \end{gathered}`

The right-angled triangles ACB and EDB,

Using the scale ratio of the sides,

`(AC)/(DE)=(CB)/(DB)=(AB)/(EB)`

`\begin{gathered} \text{Where AC=3 and DE=1} \\ AB=5\text{ and EB=unknown} \\ \end{gathered}`

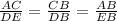
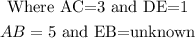
Substituting the variables,

`\begin{gathered} (3)/(1)=(5)/(EB) \\ \text{Crossmultiply} \\ 3* EB=5*1 \\ EB=(5)/(3) \end{gathered}`
`\begin{gathered} Where\text{ CB=4 and DB= unknown} \\ (3)/(1)=(4)/(DB) \\ DB=(4)/(3) \end{gathered}`

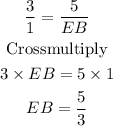
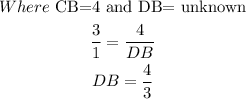
Since the ratio of the sides is AC:DE is 3:1,

Hence, the reasonable length of DE is 1 and correct option is B.