Question

Find the area of the polygon. Round the answer to the nearest tenth. Use trigonometry.

Answer 1

We are given the following triangle

To calculate the area of a triangle of base b and height h, we user the formula

`A=(b\cdot h)/(2)`

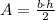
In our case we have that b=10. NOte that h is the height of the triangle. This triangle splits the triangle into two triangles, whose base are 5 and the height is h. Since the triangle is an equilateral triangle we know that each inner angle is 60 degrees. So we have the following triangle

We want to find the value of h using this triangle. With respect to the 60 degree angle, h is the opposite side and 5 is the adjacent side. So, using the tangent ration definition, we have that

`\tan (60)=(h)/(5)`

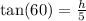
So multiplying both sides by 5, we get

`h=5\cdot\tan (60)`

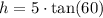
So, replacing the values of h and b in the formula, we have that

`A=(b\cdot h)/(2)=(10\cdot5\cdot\tan (60))/(2)`

Then

`A=5\cdot5\cdot\tan (60)=25\cdot\tan (60)`

Using a calculator we have that

`\tan (60)=\sqrt[]{3}`

So

`A=25\cdot\tan (60)=43.30127018`

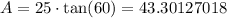
Then, rounded to the nearest tenth we have that the area of the polygon is approximately 43.3