Okay, here we have this:
According with the provided information, we are going to replace in the following formula:
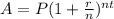
Replacing we obtain:
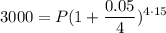
Now, let's solve for P, that is the principal investment:
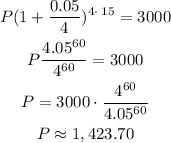
Finally we obtain that the deposit wold be aproximately of $1,423.70.