ANSWER:
a.
b.
Explanation:
We have the following functions:
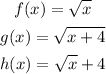
a.
We calculate all the values for each function.
For f(x):
![\begin{gathered} f\mleft(0\mright)=\sqrt[]{0}=0 \\ f(4)=√(4)=2 \\ f(8)=√(8)=2√(2) \\ f(16)=\sqrt[]{16}=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/plqca52ag5bcjfk1w0bp03rgzis4j0zd3u.png)
For g(x):
![\begin{gathered} g\mleft(0\mright)=\sqrt[]{0+4}=\sqrt[]{4}=2 \\ g(4)=\sqrt[]{4+4}=\sqrt[]{8}=2√(2) \\ g(8)=\sqrt[]{8+4}=\sqrt[]{12}=2√(3) \\ g(16)=\sqrt[]{16+4}=\sqrt[]{20}=2√(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xdy3z74oiznmw558y5q9b87ko31zsg0asp.png)
For h(x):
![\begin{gathered} h\mleft(0\mright)=\sqrt[]{0}+4=0+4=4 \\ h(4)=\sqrt[]{4}+4=2+4=6 \\ h(8)=\sqrt[]{8}+4=2√(2)+4 \\ h(16)=\sqrt[]{16}+4=4+4=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wpkvtgvu2qs4ihduk4r69a48bbwch5653u.png)
Now, we fill the table with the obtained values:
b.
To graph on the Cartesian plane, what we do is locate the points and then draw the line between these points to obtain the graph, like this: